Microcontroller Embedded C Programming Lecture 112| Bitwise right shift operator

  • Post author:
  • Post category:Blog

 

Bitwise right shift operator

 

 

 

Bitwise right shift operator ( >>)

“>>“ is a symbol you use for the right shift operator.

  • This operator takes two operands. 
  • Bitwise Right shift operator >> is used to shift the binary sequence to right side by specified position
  • Bits of the 1st operand will be right-shifted by the amount decided by the 2nd operand. So, that’s how the shift operator works. 
  • Syntax: operand1 >> operand2

 

Example

Figure 1. Example
Figure 1. Example

 

Let’s take the number 111. 

And you have to find out the value of ‘a’ which is right-shifted by 4 (a>>4).  

Here, 4 is operand2, and ‘a’ is the value(operand1), which needs to be right-shifted.  Let’s analyze this.

a = 111. I Write ‘a’ in the binary format. 

01101111 is a binary format of 111 ( which is encoded in 8 bits). 

Here ‘a’ must be right shifted by 4 times. Let’s see how it is done(Figure 2). 

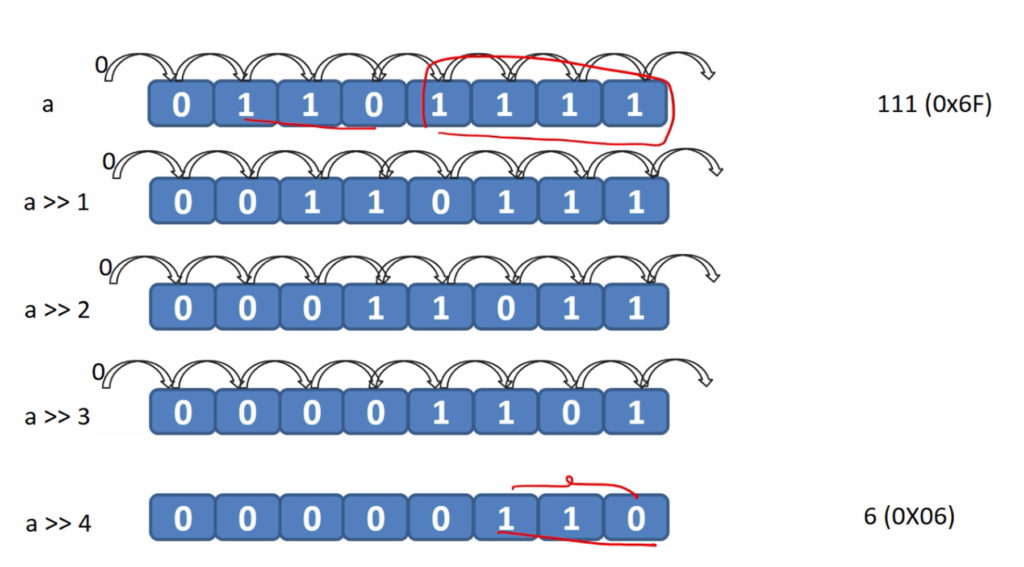
Bitwise right shift operator
Figure 2. Analyzing a>> 4 

 

01101111 is the binary number of 111. 

First, let’s see what happens when you right shift by 1. Let’s start with the least significant bit position. 

Here, the least significant number is 1, this will be right shifted. So, 1 is shifted out. That means the first bit position is lost.

After that, the second bit position is shifted to the first bit position, third bit position is shifted to the second bit position, like that. Bits will get shifted to that right. That’s why the MSB(most significant bit) will be right shifted here. That means the MSB bit position is now empty and the empty bit position will be filled with zeros. So, 0 will be shifted into the empty position, like that. 

00110111 is a result after you shift the original number by 1.

 

And after that again you shift 00110111 bits by 1. 00011011 is a result after you shift the original number by 2. Here you lost two bits.

Like that 00000110 is a result after you right shift the original value by 4. And here 1111 these four bits are actually lost in the process. So, 110 occupied the least significant bit positions, and the remaining bit positions are filled with zeros.

 

If you want to quickly find out what happens when you right shift a number by 4, then you need not analyze it like this(Figure 2). So, there is a shortcut(as shown in Figure 3).

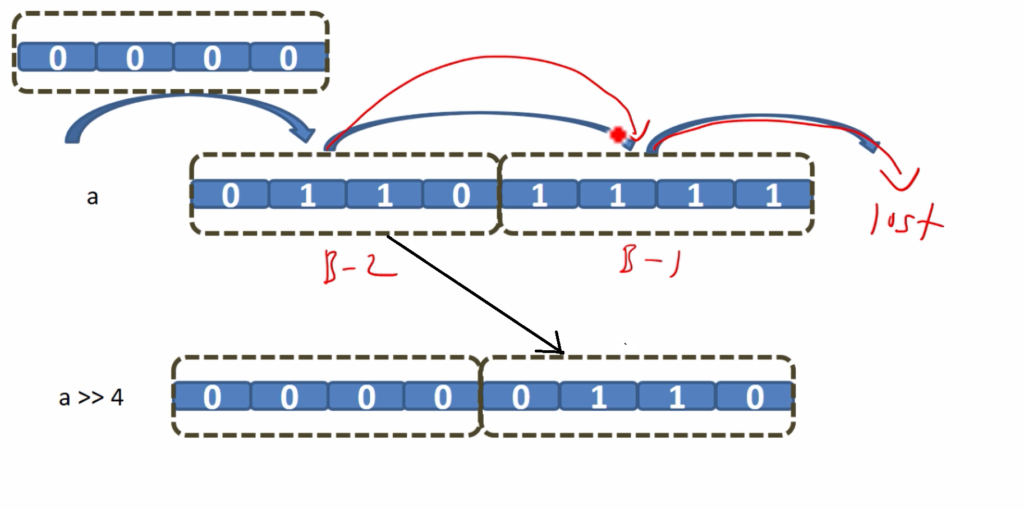
Bitwise right shift operator
Figure 3. Shortcut method

 

First, take the original number and it is right-shifted by 4. That’s why create a block of 4 bits. 1111 is a block1 and 0110 is a block2. So, block1 is a collection of 4 bits and block2 is a collection of 4 bits. And then shift this block1 out. Block1 is lost.

After that, shift the block2 in. block2 comes to block1’s position, and for the remaining bits, you just write zeros. You can also analyze it like this.

 

For example, a>>3.

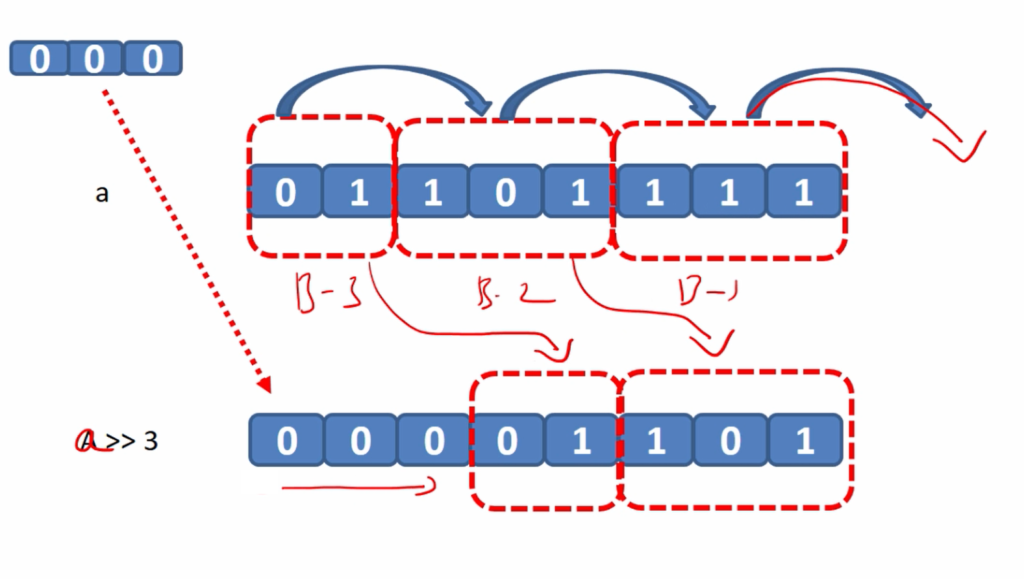
Bitwise right shift operator
Figure 4. Example

 

First, create blocks of three bits. 

111 is block1, 101 is block2, and 01 is block3. And in block3 you can keep only 2 bits.

After the right shift, 111 is lost(block1). Then, 101 comes to block1’s position, and 01 comes to block2’s position. And since 3 bits are lost, there will be three empty places, so make it 0 those empty places.

00001101 is a result you get after your right shift ‘a’ by 3. So, that’s how the right shift happens. 

In the following article, let’s discuss Bitwise left-shift operator.

 

FastBit Embedded Brain Academy Courses

Click here: https://fastbitlab.com/course1

 

Tags:

FastBitLab

The FastBit Embedded Brain Academy uses the power of internet to bring the online courses related to the field of embedded system programming, Real time operating system, Embedded Linux systems, etc at your finger tip with very low cost. Backed with strong experience of industry, we have produced lots of courses with the customer enrolment over 3000+ across 100+ countries.