Microcontroller Embedded C Programming Lecture 102| Applicability of bitwise operators : Clearing of bits

  • Post author:
  • Post category:Blog

 

Applicability of bitwise operators : Clearing of bits

 

 

 

In this article, let’s learn about the Clearing of bits. 

Write a program to clear(make bit state to 0) the 4th, 5th, 6th, bit positions of a given number and print the result. 

 

First, which bitwise operation do you use to clear the given bit position of data? Do you use the bitwise & or bitwise | operator? 

‘&‘ is used to ‘TEST and CLEAR’ not to ‘SET.’

‘|‘ is used to ‘SET’ not to ‘TEST.’ 

 

In this case, certainly, we cannot use bitwise OR (|) because that is used to SET. So, you have to use bitwise & operator. So, bitwise ‘&’ is used to ‘TEST and CLEAR’. 

 

Now let’s see how we can do that. The goal is to reset the 4th, 5th, and 6th bit positions.

Figure 1. Exercise
Figure 1. Exercise

 

You should also be careful that the bit positions from 0 to 3 should not be affected, and also, the bit position 7 should not be affected. So, we select a mask value that helps you to 0 out the required portion.

For example, the data is 10111110, and the 4th, 5th, and 6th portions must be zeroed out here. That’s why we keep this portion of the mask value as zero’s, and the remaining bit positions of the given data should not be affected. That’s why let’s mask those data portions with 1’s. So, in this case, 10001110 ( the mask value) turns out to be 0x8F.  

Observe the output. Only the 4th, 5th and 6th portions are zeroed out, so the 7th portion and 0 to 3 portion are not affected, as shown in Figure 1. So, the takeaway from this post is bitwise & is used to both ‘TEST’ and ‘CLEAR’.

 

There is one more method you can use to clear the bits.

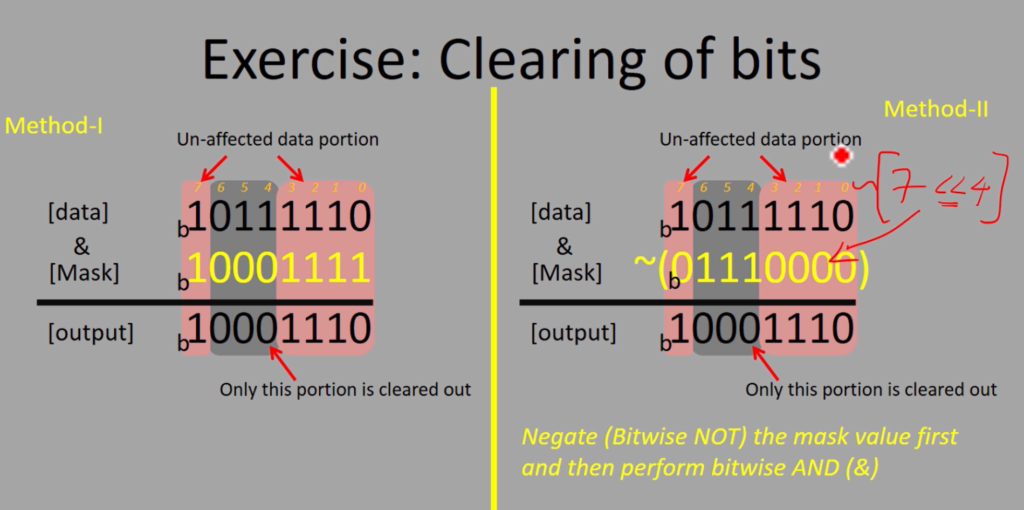
Applicability of bitwise operators : Clearing of bits
Figure 2. Exercise

 

Method-1 is shown in Figure 1. Here, the mask value should be 1 for the unaffected data portion of the data, and use zeroes in the mask value to zero out the required bit positions.

And here in method-2, you use a combination of the bitwise & and the negation(~), that is bitwise NOT. 

In this case, negate the mask value first and then perform the bitwise &. Here, 01110000 is the mask value, and you negate that. When you negate that, the final output is 10001110.  

In method 1, you need to think to decide the mask value, and you have to work it out and then calculate how much it is. 10001111 is 0x8F.

For example, in method 2, I want to zero out the data’s 4th, 5th, and 6th-bit positions. That means 3-bit positions. So, I can immediately guess the number 7. 7 means 111 in binary.

After that, what I do is, I left-shift(<<) 7 by 4. Because I know that I need to clear out the bits from the 4 bit onwards, that’s why I left shift by 4. 

7<<4 gives you a 01110000 number. After that, you negate that. When you negate that, this whole thing will give you a 10001111 number.

 

The advantage of method 2 is that you need not to think too much. That’s why this method is more convenient, but don’t worry if it confuses you while doing exercises, it will get cleared. To appreciate this method, you also have to learn the bitwise shift operator.

 

FastBit Embedded Brain Academy Courses

Click here: https://fastbitlab.com/course1

 

Tags:

FastBitLab

The FastBit Embedded Brain Academy uses the power of internet to bring the online courses related to the field of embedded system programming, Real time operating system, Embedded Linux systems, etc at your finger tip with very low cost. Backed with strong experience of industry, we have produced lots of courses with the customer enrolment over 3000+ across 100+ countries.