Range calculation for ‘char’ data type
In this article, let’s discuss the range calculation of char data type.
- We know that variable of the char data type consumes 1 byte of memory.
- Also, the char data type will be used to store 1 byte of signed data.
1 byte signed data representation:
Let’s see how signed data will be stored in 1 byte of computer memory. Let’s start with 1 byte signed data representation.
1 byte means 8 bits. Out of 8 bits, the most significant bit will be used to represent the sign of the data. If it is 0, then the data is considered positive. If it is 1, then the data is considered negative. And if the 7th bit or the most significant bit is 1, then the data is considered negative. And the remaining 7 bits are used to store the magnitude.
Magnitude is stored in 2’s complement format if data is negative.
Signed data means a dedicated 1 bit is used to encode a sign of the data.

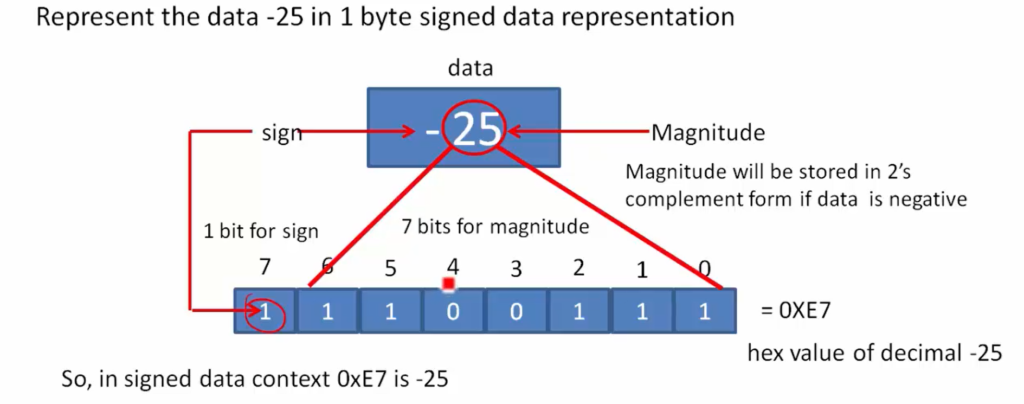
Let’s see an example. Represent the data -25 in 1 byte signed data representation.
So, the data given is -25. It has two parts. One is a sign, and another one is magnitude. The sign is negative(-), and the magnitude is 25. Since the data is negative, the magnitude will be stored in 2’s complement form. You have to remember that. So, out of 8 bits, the seventh bit, that is the most significant bit, will be 1 in this case. And the remaining 7 bits are used to store the magnitude that is 25 in 2’s complement form. Let’s see how we can do that.
First of all, the data given is -25. Here let’s represent the magnitude that is 25 in binary format.

The binary form of 25 is 11001. 1’s complement of binary 25 is 00110.
To represent 25, you at least need 5 bits. But it is 1 byte representation, so there will be the remaining 3 bits. Let’s consider them as 0. 00011001 is a representation for 25 or +25.
Now, let’s take the 1’s complement of this binary format. So now, it will be 11100110. This is a 1’s complement form of 25.
Let’s take the 2’s complement form of this. So, you have to add 1 to this. 11100111 is a 2’s complement form of 25.
We finally got this number, which is 11100111. This is 1 byte data. And observe the 7th bit, which is 1 (see Figure 2). So, this is a sign bit that represents data is negative.
The 7th bit is a sign bit, and the remaining bits are the magnitude. So, magnitude for 25 in 2’s complement form.
If I convert -25 into hex form, what happens?
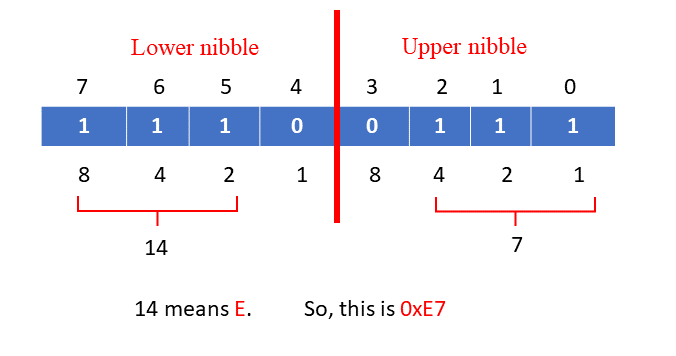
1110 is a lower nibble, and 0111 is an upper nibble. 1110 turns out to be 7, and 1110 turns out to be 14. 14 means E. 11100111 turns out to be 0xE7. 0xE7 is the hex value of decimal -25.
It is very very simple. Remember that, in signed data representation, a dedicated 1 bit is reserved in order to encode the sign, and you are left with only seven bits to represent the magnitude.
Now let’s see another example. Represent the data 25 in 1 byte signed data representation. That is +25.
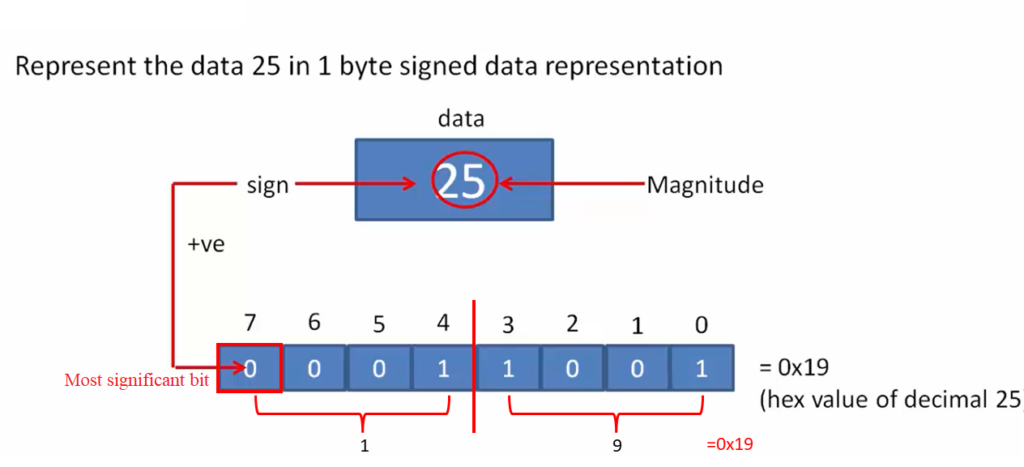
Here the sign is positive. That’s why the most significant bit will be 0. And since the data is positive, you need not convert the magnitude into 2’s complement form. So, you convert that into the binary format here. 00011001 is the binary format of 25.
If I convert 00011001 into hex, 1001 will be 9, and 0001 will be 1. So, that happens to be 0x19, which is a hex value for decimal +25.
Now, based on that, let’s discuss the char data type range.

When the sign is positive, the seventh bit will be zero. So the least value that we can store is all zeroes. That’s why the magnitude will be 0. That is the least possible magnitude.
And the highest value would be to fill all the magnitude bits with 1. That’s why the highest positive value would be 127.

When the sign is negative, the seventh bit will be 1. The least value possible is -128. -128 means all magnitude bits are filled with zeros. So, 10000000 is the 2’s complement format for -128.
And the highest negative value possible is -1. So, when it is -1, all the magnitude bits are filled with 1. 11111111 is the 2’s complement format for -1.
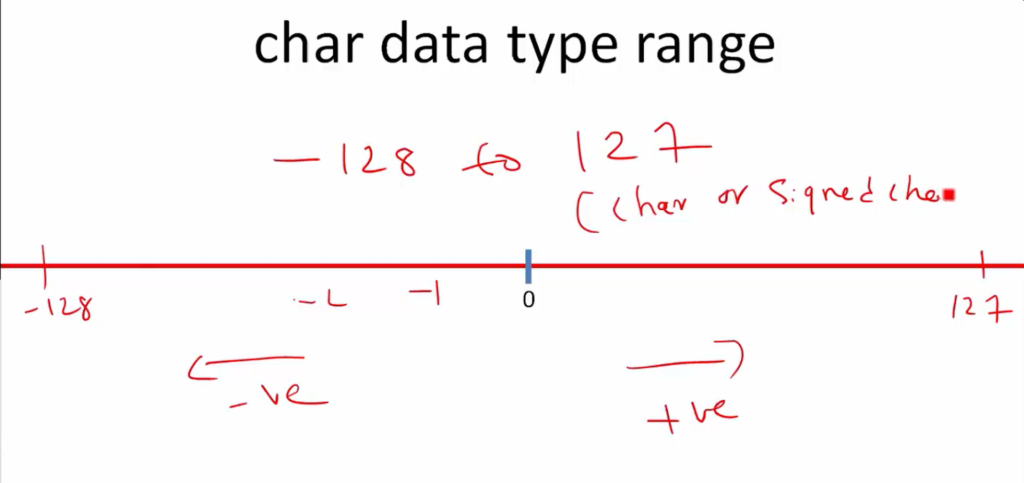
Now we have here two ranges for positive values and negative values. For positive values, it can go from 0 to 127. For negative values, the range would be 0 to -128. So, the range of char data type is -128 to 127. This is a range for char or signed char(Figure 8).
Unsigned char range:
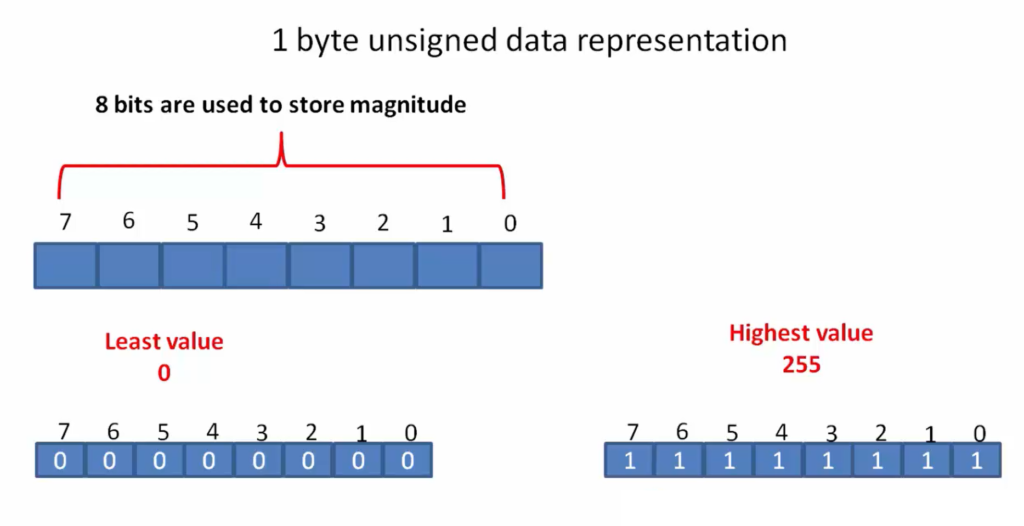
- The unsigned char data type is used to store 1 byte of unsigned data.
- In unsigned data representation no particular bit is dedicatedly used to encode the sign.
FastBit Embedded Brain Academy Courses
Click here: https://fastbitlab.com/course1